Memory usage is well-defined for Java on your computer that every value requires precisely the same amount of memory each time that you run your program. But Java is implemented on a very wide range of computational devices, and memory consumption is implementation-dependent. So, following is some typical values that subject to machine dependencies.

One of Java’s most significant features it its memory allocation system, which is supposed to relieve you from having to worry about memory. Certainly, you’re well-advised to take advantage of this feature when appropriate. Still, it is your responsibility to know, at least approximately, when a program’s memory requirements will prevent you from solving a given problem.

Typical Java implementations use 4 bytes (32 bits) to represent int values, representing each char value with 2 bytes (16 bits), each double and each long value with 8 bytes (64 bits), and each boolean value with 1 byte (since computers typically access memory one byte at a time). Combined with knowledge of the amount of memory available, you can calculate limitations from these values. For example, if you have 1GB of memory on your computer (1 billion bytes), you cannot fit more than about 32 million int values or 16 million double values in memory at any one time.

typical memory requirements for primitive types in Java

On the other hand, analysing memory usage is subject to various differences in machine hardware and in Java implementations, so you should consider the specific examples that we give as indicative of how you might go about determining memory usage when warranted, not the final word for your computer. For example, many data structures involve representation of machine addresses, and the amount of memory needed for a machine address varies from machine to machine. For consistency, the following context assume that 8 bytes are needed to represent addresses, as is typical for 64-bit architectures that are now widely used, recognizing that many older machines use a 32-bit architecture that would involve just 4 bytes per machine address.

Objects

To determine the memory usage of an object, we add the amount of memory used by each instance variable to the overhead associated with each object, typically 16 bytes. The overhead includes a reference to the object’s class, garbage collection information, and synchronization information. Moreover, the memory usage is typically padded to be a multiple of 8 bytes (machine words, on a 64-bit machine). For example, an Integer object uses 24 bytes (16 bytes of overhead, 4 bytes for its int instance variable, and 4 bytes of padding). Similarly, a Date object (defined in algs4.jar) also uses 32 bytes: 16 bytes of overhead, 4 bytes for each of its three int instance variables, and 4 bytes of padding. A reference to an object typically is a memory address and thus uses 8 bytes of memory. For example, a Counter object (as shown in following figure) uses 32 bytes: 16 bytes of overhead, 8 types for its String instance variable (a reference), 4 bytes for its int instance variable, and 4 bytes of padding. When we account for the memory for a reference, we account separately for the memory for the object itself, so this total does not count the memory for the String value.

Linked lists

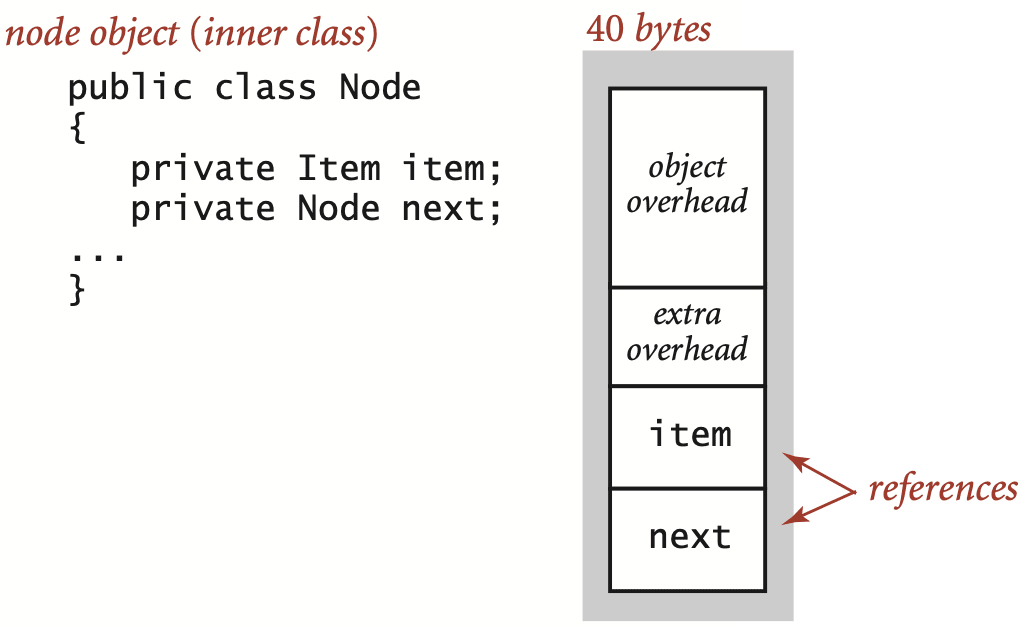
A nested non-static (inner) class such as the Node class requires an extra 8 bytes of overhead (for a reference to the enclosing instance). Thus, a Node object uses 40 bytes (16 bytes of object overhead, 8 bytes each for the references to the Item and Node objects, and 8 bytes for the extra overhead). Thus, since an Integer object uses 24 bytes, a stack with N integers built with a linked-list representation uses 32 + 64N bytes, the usual 16 for object overhead for Stack, 8 for its reference instance variable, 4 for its int instance variable, 4 for padding, and 64 for each entry, 40 for a Node and 24 for an Integer.

Arrays

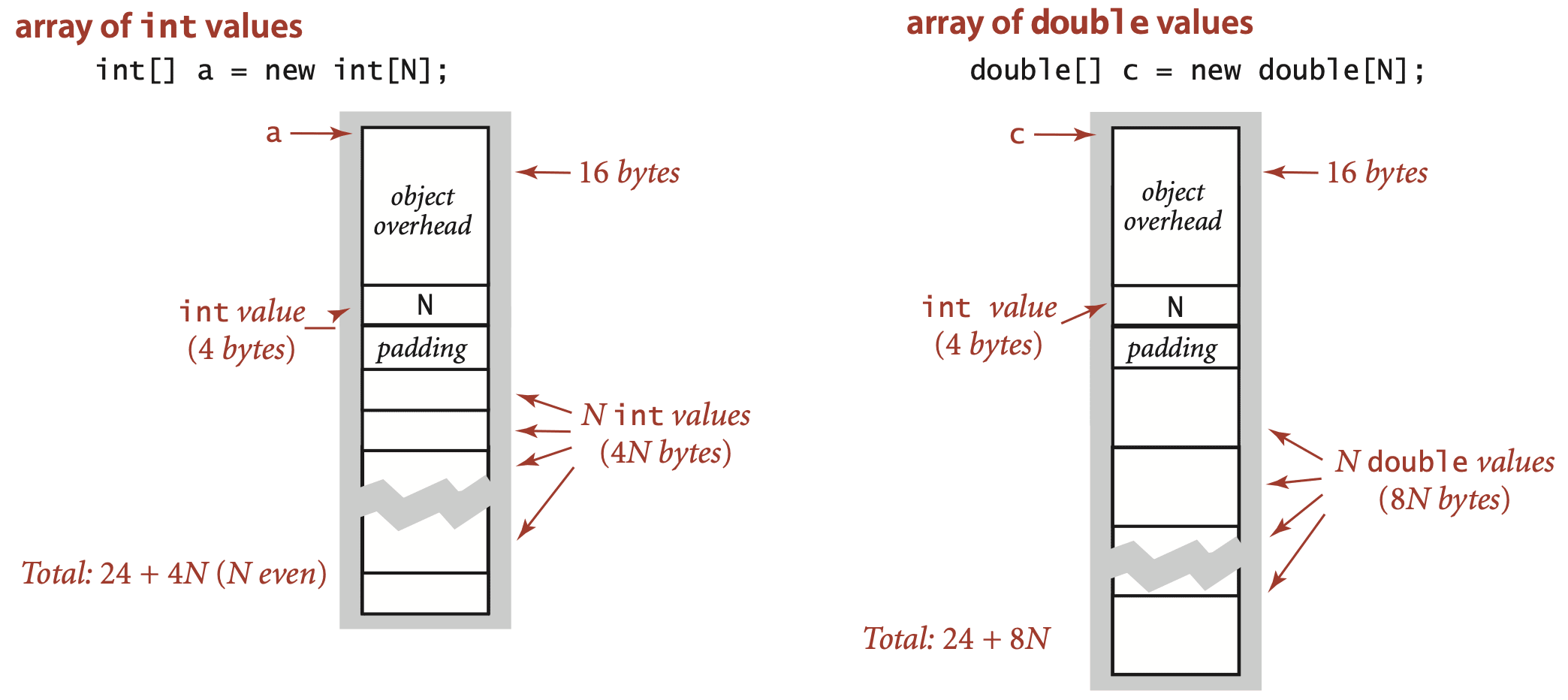
Arrays in Java are implemented as objects, typically with extra overhead for the length.

An array of primitive-type values typically requires 24 bytes of header information (16 bytes of object overhead, 4 bytes for the length, and 4 bytes of padding) plus the memory needed to store the values. For example, an array of N int values uses 24 + 4N bytes (rounded up to be a multiple of 8), and an array of N double values uses 24 + 8N bytes.

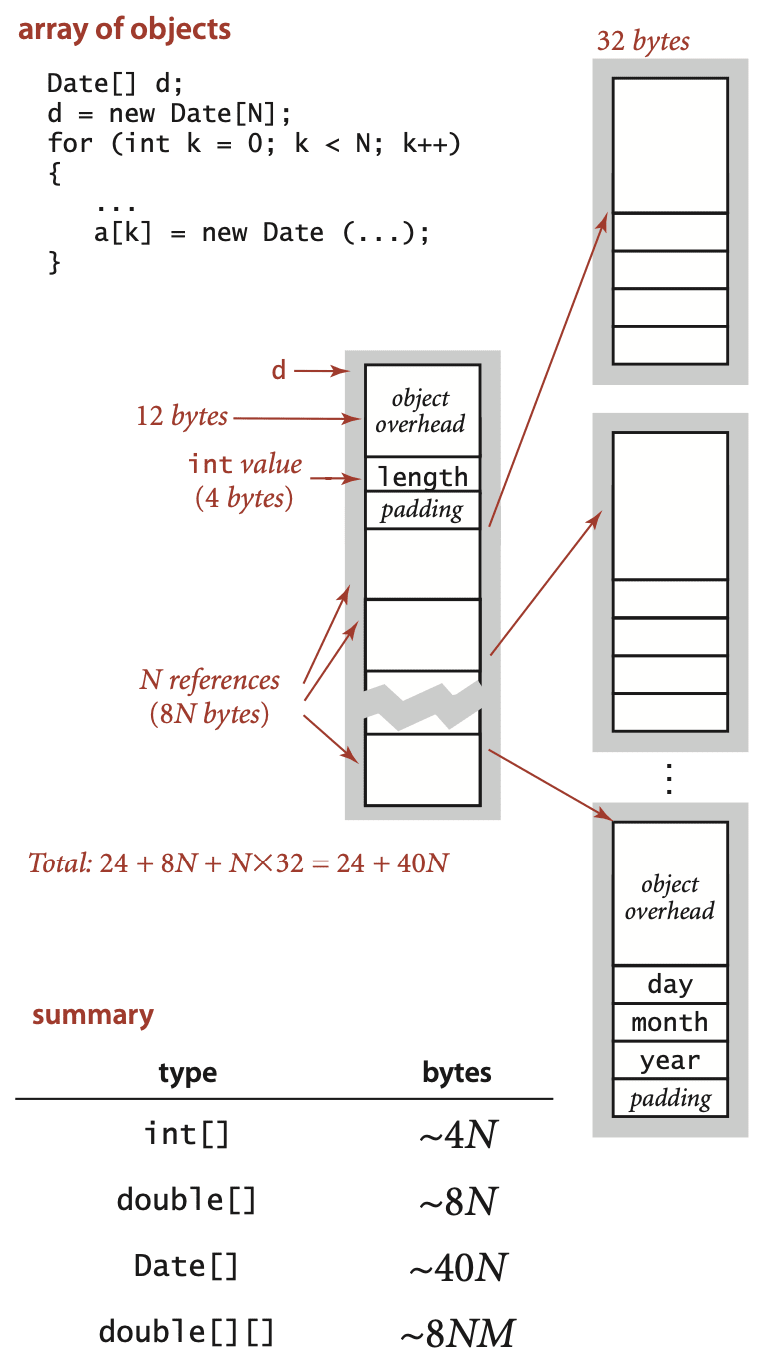
An array of objects is an array of references to the objects, so we need to add the space for the references to the space required for the objects. For example, an array of N Date objects uses 24 bytes (array overhead) plus 8N bytes (references) plus 32 bytes for each object and 4 bytes of padding, for a grand total of 24 + 40N bytes. A two-dimensional array is an array of arrays (each array is an object). For example, a two-dimensional M-by-N array of double values uses 24 bytes (overhead for the array of arrays) plus 8M bytes (references to the row arrays) plus M times 16 bytes (overhead from the row arrays) plus M times N times 8 bytes (for the N double values in each of the M rows), for a grand total of 8NM + 32M + 24 ~ 8NM bytes. When array entries are objects, a similar accounting leads to a total of 8NM + 32M + 24 ~ 8NM bytes for the array of arrays filled with references to objects, plus the memory for the objects themselves.

String objects

We account for memory in Java’s String objects in the same way as for any other object, except that aliasing is common for strings. The standard String implementation has four instance variables: a reference to a character array (8 bytes) and three int values (4 bytes each). The first int value is an offset into the character array; the second is a count (the string length); the third is a hash code that saves re-computation in certain circumstances that need not concern us now. Therefore, each String object uses a total of 40 bytes (16 bytes for object overhead plus 4 bytes of padding). This space requirement is in addition to the space needed for the characters themselves, which are in the array. The space needed for the characters is accounted for separately because the char array if often shared among strings. Since String objects are immutable, this arrangement allows the implementation to save memory when String objects have the same underlying value[].

String values and substrings

A String of length N typically uses 40 bytes (for the String object) plus 24 + 2N bytes (for the array that contains the characters) for a total of 64 + 2N bytes. But it is typical in string processing to work with substrings, and Java’s representation is meant to allow us to do so without having to make copies of the string’s characters. When you use the substring() method, you create a new String object (40 bytes) but reuse string takes just 40 bytes. The character array containing the original string is aliased in the object for the substring; the offset and length fields identify the substring. In other words, a substring takes constant extra memory and forming a substring takes constant time, even when the lengths of the string and the substring are huge. A naive representation that requires copying characters to make substrings would take linear time and space. The ability to create a substring using space (and time) independent of its length is the key to efficiency in many basic string-processing algorithms.

These basic mechanisms are effective for estimating memory usage of a great many programs, but there are numerous complicating factors that can make the task significantly more difficult. We have already noted the potential effect of aliasing. Moreover, memory consumption is a complicated dynamic process when function calls are involved because the system memory allocation mechanism plays a more important role, with more system dependencies. For example, when your program calls a method, the system allocates the memory needed for the method (for its local variables) from a special area of memory called stack (a system pushdown stack), and when the method returns to the caller, the memory is returned to the stack. For this reason, creating arrays of other large objects in recursive programs is dangerous, since each recursive call implies significant memory usage. When you create an object with new, the system allocates the memory needed for the object from another special area of memory known as the heap, and you must remember that every object lives until no references to it remain, at which point a system process known as garbage collection reclaims its memory for the heap. Such dynamics can make the task of precisely estimating memory usage of a program challenging.